La empresa Turistas-A-Cholón (TAC) está especializada en autobuses de dos pisos para recorridos turísticos. Raimundo Revisor tiene una aburrida tarea: debe revisar todos los autobuses que salen de la parada inicial a lo largo del día y comunicar a la central cuántos turistas hay en el piso superior y cuántos en el piso inferior.

Sin embargo, Raimundo Revisor está cansado de estos repetitivos mensajes y ha ideado un método más compacto para describir los turistas que hay en cada piso: en lugar de transmitir las dos cantidades transmite un único número (llamado rango) que resume perfectamente la ocupación del autobús. Para ello sigue el siguiente esquema (donde el rango de cada autobús aparece a su lado), distribuyendo en filas los autobuses con el mismo número de turistas totales.

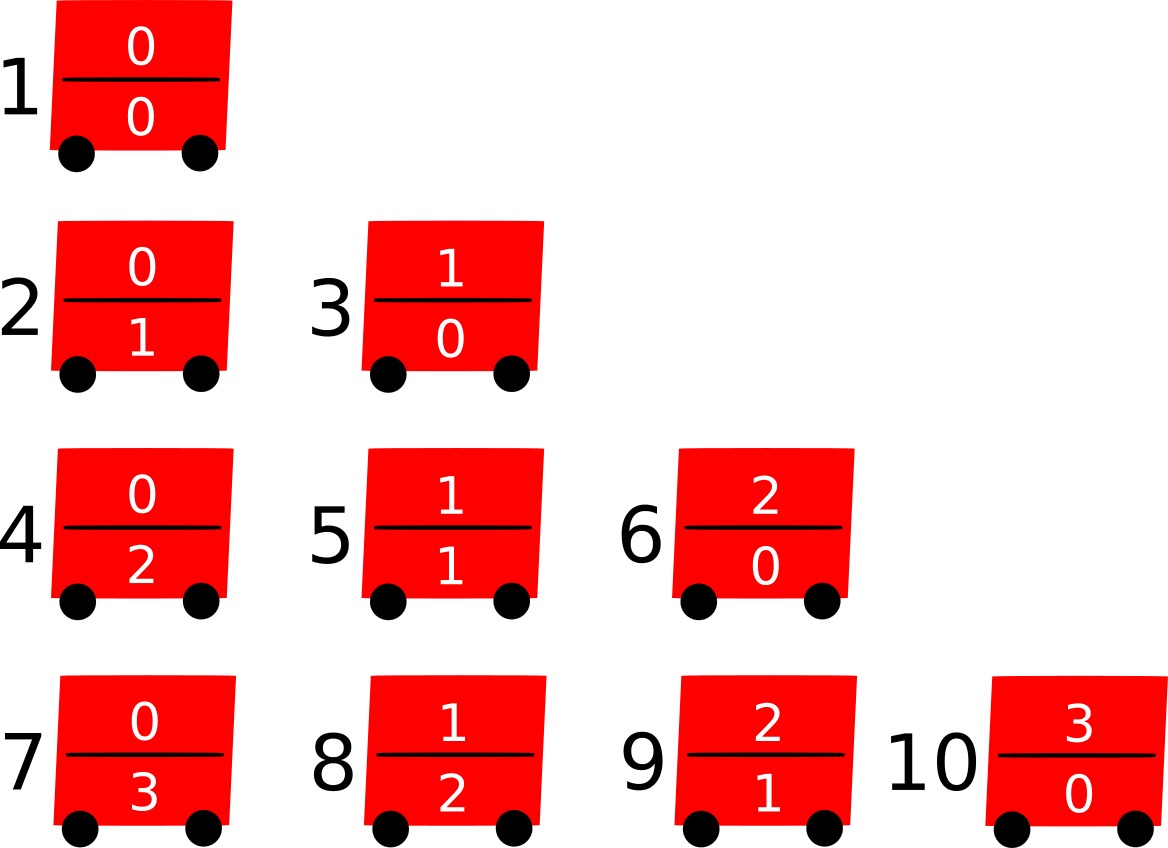
Raimundo no tiene aún mucha pericia, y necesita un programa para calcular el rango de un autobús en base al número de turistas que transporta en cada piso.

Entrada

La primera línea contiene el número A de autobuses para calcular su rango. Luego siguen A líneas con el formato N M, donde N es el número de turistas que viajan en el piso superior y M el número de turistas en el piso inferior. La máxima ocupación de cada piso es 1.000.

Salida

Para cada caso de prueba, el programa escribirá el rango del autobús.

Entrada de ejemplo

3
0 0
1 2
2 0

Salida de ejemplo

1
8
6

Solución propuesta

def gauss(n):
    return (n + 1) * n / 2


def pares(n):
    lista = []
    for x in range(0, n + 1):
        lista.append([x, n - x])
    return lista


if __name__ == '__main__':
    casos = int(input())
    respuestas = []
    for caso in range(casos):
        par = [int(x) for x in input().split(' ')]
        total = sum(par)
        previos = int(gauss(total))
        lista = pares(total)
        respuestas. append(previos + lista.index(par) + 1)
    for respuesta in respuestas:
        print(respuesta)

Este ejercicio puede parecer un poco lioso al leerlo, pero aplicando el principio de divide y vencerás o modularizando se resuelve muy fácilmente. Hay que tener en cuenta que lo que hay que hacer es la posición que ocupa el par que nos dan. Dicha posición se calcula formando el triángulo, donde podemos visualizarlo como un triángulo divido por niveles, que será la suma del par es decir, dado el par (i, j) el nivel será n = i + j.

Por otro lado, en cada nivel los pares se ordenan desde el (0, n) hasta el (n, 0), de modo que podemos generar la lista de los pares y contar que nos han dado.

Ahora vamos a explicar el código. La parte del main es bastante sencilla, ya que lo que hacemos es leer el par, calcular la suma de dicho par, y llamar a un par de funciones.

La función gauss, lo que calcula es la suma gaussiana, que por si no la conocéis lo que se calcula es la suma de los n primeros números es decir, la suma de 1 a n. Se debe al matemático Gauss y no es más que aplicar la fórmula. ¿Para qué queremos esta suma? Pues para poder saber cuántos pares tenemos en los niveles anteriores al par en el que estamos.

Posteriormente, generamos la lista de los pares anteriormente mencionados, es decir, la lista de pares de (0, n) a (n, 0), y después lo único que hay que hacer es recuperar el índice de dicho par y sumarle 1 por supuesto, ya que el índice irá desde 0 a la longitud de la lista menos 1.

Poco más tiene este ejercicio, una vez se codifican las dos funciones el resto está hecho.

Enlace del código

Enlace en aceptaelreto.com