Dado un conjunto (o muestra) de valores positivos ordenados, se define la mediana como el valor que ocupa la posición central de los datos dados:

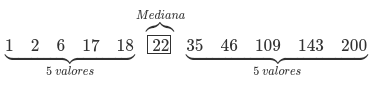
En el caso de tener un número impar de valores, la mediana está clara: será aquel valor que tenga el mismo número de valores más pequeños y más grandes que él en la muestra. En el caso de tener un número par de valores, habría dos candidatos a ser mediana. En vez de decidirnos por uno, en este caso la mediana viene dada por la media aritmética de esos dos valores que ocupan las posiciones centrales.

Dada una colección de números positivos, nos piden calcular la mediana. Para evitar tener que trabajar con números decimales en algunos casos, habrá que calcular su doble.

Entrada

La entrada consta de una serie de casos de prueba. Cada uno comienza con un número, menor o igual que 25.000, que indica la cantidad de valores que tiene la muestra. A continuación se dan los valores de la muestra, todos números enteros positivos, de los que habrá que calcular la mediana multiplicada por dos.

La entrada terminará con una serie de 0 valores.

Salida

Para cada caso de prueba se mostrará el doble de la mediana de los valores dados.

Entrada de ejemplo

11
1 2 6 17 18 22 35 46 109 153 200
5
5 3 1 2 8
4
4 5 9 2
0

Salida de ejemplo

44
6
9

Solución propuesta

from statistics import median

if __name__ == '__main__':
    soluciones = []
    tamaño_muestra = int(input())
    while tamaño_muestra:
        muestras = [int(x) for x in input().split(' ')]
        soluciones.append(median(muestras) * 2)
        tamaño_muestra = int(input())
    for solucion in soluciones:
        print(solucion)

En este ejercicio, voy a aprovechar para explicar una instrucción nueva, la cual no vamos a utilizar en nuestro código directamente pero sí que es imprescindible posteriormente.

Primero hay que tener en cuenta que hay muchas funciones y clases que forman parte del núcleo del lenguaje, como son input(), print(), list, y todas las que hemos utilizado hasta ahora. Sin embargo, hay muchas otras funciones que podemos utlizar pero son externas de modo que hay que llamarlas. Pero, resultaría tedioso tener que llamarlas una a una, así que se agrupan en librerías.

Si queremos importar toda una librería, se utiliza la instrucción import “libreria” y para utilizar una función de dicha libería se utlizaría libreria.funcion:

import math
math.sqrt(2)

Pero hay nombres de librerías que pueden ser más largos y se puede renombrarlas dentro de nuestro código con las instrucción as:

import numpy as np
import pandas as pd

Por último, si como en el ejercicio de hoy sabemos que solo vamos a utilizar una función, podemos importar solo ésta, como vemos en nuestro código, from libreria import funcion.

Si queremos conocer todas las funciones que hay en la librería, podemos acudir a la documentación oficial de dicha libreria en nuestro caso, Mathematical statistics functions, cuya inclusión se produce en la versión 3.4.

Por último y debido a que Python es de código abierto, el código de dicha librería se encuentra disponible y podmeos ver la implementación de la función mediana:

def median(data):
    """Return the median (middle value) of numeric data.
    When the number of data points is odd, return the middle data point.
    When the number of data points is even, the median is interpolated by
    taking the average of the two middle values:
    >>> median([1, 3, 5])
    3
    >>> median([1, 3, 5, 7])
    4.0
    """
    data = sorted(data)
    n = len(data)
    if n == 0:
        raise StatisticsError("no median for empty data")
    if n%2 == 1:
        return data[n//2]
    else:
        i = n//2
        return (data[i - 1] + data[i])/2

Fuente: statistics.py

Enlace del código

Enlace en aceptaelreto.com